개인적인 생각을 정리한 것으로 오류가 많으니 공신력있는 문서를 참고 부탁드립니다....
카이제곱 분포는 참 많이 사용된다.
특히 사회과학 가설검정에서 직간접적으로 사용되는데 카이제곱분포가 가지는 의미를 알면 왜 사용되는지 추정하기 편하다.
카이제곱은 "정규분포에서 랜덤하게 df개 만큼 뽑아 제곱해서 더한 것의 분포이다.
키워드를 뽑아보면 정규분포, 제곱, 더한것인 것 같다.
좀 다른 이야기를 해보면 우리가 모델을 만들고 검정을 할 때 중요한 것 중 하나는 "오차"다. 즉 예측과 실제값이 얼마나 다른가 이다. 그런데 추론통계(glm)은 모든 변수들이 정규성을 따른다고 본다. 그렇다면 예측값-실제값은 정규분포 - 정규분포이다. 정규분포서 다른 정규분포를 빼면 그 또한 정규 분포를 따른다. 즉 오차도 정규성을 따른다(따라야 하는게 회귀분석 전재다.).
다만 이 오차를 다 더하면 0이 된다. 아래 예를 보자
| 실제 | -5 | -2 | 2 | 5 |
| 예측 | -7 | -1 | 1 | 7 |
| 오차 | -2 | 1 | -1 | 2 |
그래서 오차가 얼마나 있는지 알기 위해서 제곱을 한다음에 더한다. 평균편차를 사용하지 않고 표준편차를 사용하는 이유와 같다.
이 경우 이 오차의 합을 잘 보면 정규분포를 따르는 df개의 값을 제곱해서 더해준 것과 같다. 즉 카이제곱 분포를 따른다는 것이다.
종합하면 오차의 합은 카이제곱 분포를 따른다는 것이다.
시뮬래이션을 돌려보자
-정규분포에서 1개만 뽑았을 때 분포이며 sample 수만 조정 하면 된다.
z<-rnorm(100000)
sum((sample(z,10))^2)
x2<-c()
for (i in 1:1000) {
x2[i]<-sum((sample(z,1))^2)
}
hist(x2, freq = F, breaks = 100, main = "자유도 1")
lines(density(x2), col="red", lwd =3)


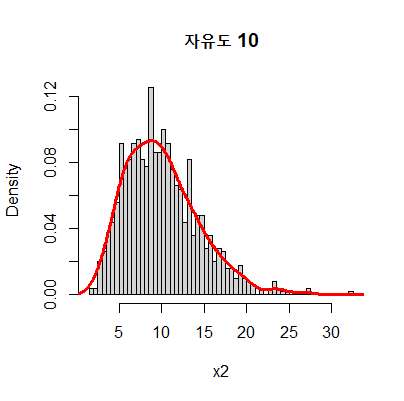
조금 더 나아가보자. F검정을 하기 위해 F분포를 사용하는데 F분포 또한 카이제곱분포처럼 검색하면 모양이 자유도에 따라 다르다. 그러나 공식을 보면 당연하다.
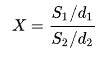
s는 오차합(변량분석으로 치면 Sum Square)으로 카이제곱분포이다. 하나의 카이제곱 분포를 자유도로 나눈 값을 각각 나누면 그 모양이 대략 카이제곱 분포가 된다. 좀더 거칠게 말하면 카이제곱 두개를 나눈 값이니 모양이 카이제곱스러워지는 것이다.
이를 통해 F분포의 의미도 생각해볼 수 있다. 두 오차의 비율의 분포가 F분포가 된다.
'기타 잡기장' 카테고리의 다른 글
| [R]카이제곱분포 분포도 (0) | 2023.05.02 |
|---|---|
| 연속형 변수 ~ 범주형 변수(외래관광실태조사) (0) | 2022.12.05 |
| hayes model 5(조건부 직접효과) (0) | 2022.11.30 |
| hayes model 4(매개모형) (0) | 2022.11.30 |
| hayes model 3 (0) | 2022.11.28 |


댓글